Sponsored Links
Ok. You don't have to calculate the volume of the point or the missing parts around it.
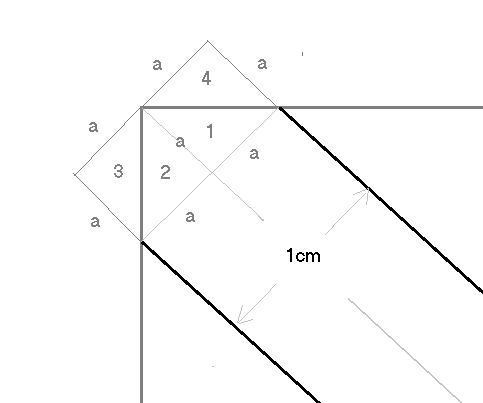
2D diagram:
All sides 'a' are 0.5cm.
The missing triangles '3' and '4' are the same size as triangles '1' and '2' - so must be the same as the equivalent '1' and '2' at the other end of the hole.
Therefore if you deduct just one 'a' from the vortex to vortex length (17.32 - 0.5 = 16.82), you actually have the area of the missing part
Therefore, by extension, this must also apply 3D cubes.
In cuboids, though , where the entry and exit angle will not be 45°, you would have to calculate 'a' (well, we have in your example; it was just very easy).
2D diagram:
All sides 'a' are 0.5cm.
The missing triangles '3' and '4' are the same size as triangles '1' and '2' - so must be the same as the equivalent '1' and '2' at the other end of the hole.
Therefore if you deduct just one 'a' from the vortex to vortex length (17.32 - 0.5 = 16.82), you actually have the area of the missing part
Therefore, by extension, this must also apply 3D cubes.
In cuboids, though , where the entry and exit angle will not be 45°, you would have to calculate 'a' (well, we have in your example; it was just very easy).
Vertex - not vortex - sorry.
Can't be bothered to alter them all.
Can't be bothered to alter them all.
B
Bodd
Do we have an answer ?
Sponsored Links
E
EddieM
Sorry, it's a cylinder going through it, more complex I am afraid.
E
EddieM
Hmm not sure, for me Pip's is certainly on the right track, and could well be the right answer.
B
Bodd
And his answer was?
E
EddieM
I guess 97.52% remains, can't prove it though.
B
Bodd
B
Bodd
That's what pip said
Yes, you are right.
I just had an Archimedes moment while in the bath.
I did ,though, get the same answer as Magicmushroom and his CAD.
More thinking.
E
EddieM
fret ye not. Understanding the problem itself is quite challenging, let alone the answer!
If you take the vertex to vertex measurement of 17.32 (are we agreed on that?) and calculate a cylinder - including the actually missed parts - then that cylinder is 13.60 cu.cm.
That is 1000 - 13.60 = 986.4 therefore the true answer MUST be higher than 98.64%.
That is 1000 - 13.60 = 986.4 therefore the true answer MUST be higher than 98.64%.
- Joined
- 28 Jul 2014
- Messages
- 1,968
- Reaction score
- 561
- Country
I think the only way to calculate this, is to take that 'new cylinder' and cut it into three 120° strips...
Then, we need to cut off a chip, at, I think, 35.26 degrees (because that's the angle of a right triangle of side √2 and hypotenuse √3)...
(i.e. if you had three of these and put them together, you would get a 'cube corner ended cylinder')
Doesn't mean I know how to actually give an answer still!! But once we know the volume of that 'chip', we can times that by six and take that away from the 'new cylinder' mentioned before.
Last edited:
Sponsored Links
