Honeywell cm927 thermostat

[mikely]

If the boiler is being turned off, even for a short time, there can't be a constant output, so there will inevitably be a change in temperature in the house.

No, there isn’t a constant output, but the time averaged output of the system when working in time proportional mode can be constant. To look at it another way, in steady state conditions, the amount of energy put into the building per hour is constant and therefore the temperature is constant. In steady state conditions this is what the TPI controller achieves, a time averaged heating output that balances the heat loss to give a constant temperature. As you say there will be small temperature variations between heating cycles but the long term average will generally be more accurate than a simple on/ off thermostat.

Quoting from the Honeywell homexpert web site FAQ:
How does TPI Control work?
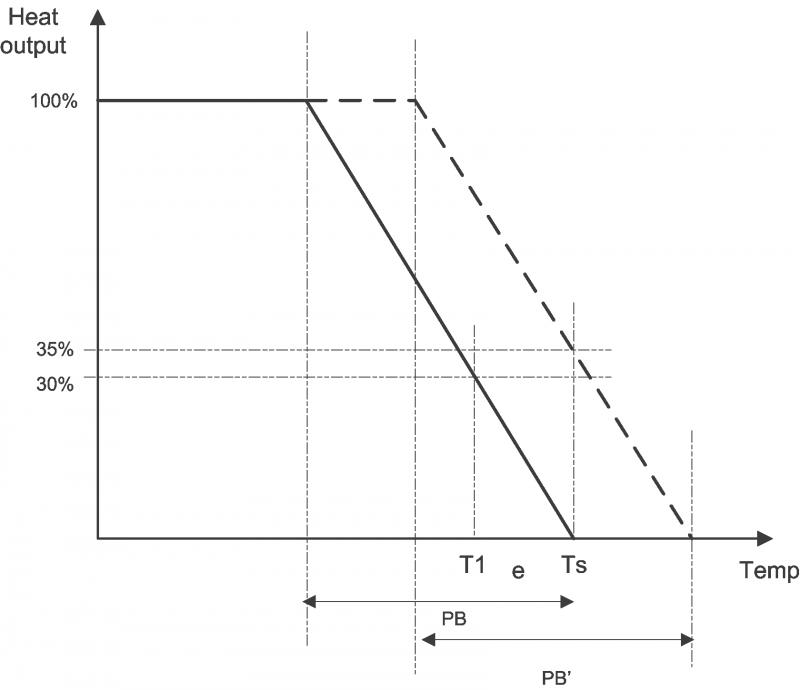
A thermostat operates using a fixed number of firing periods per hour (normally selected to suit the appliance and system). This can often mean a thermostat can fire the boiler even when the set temperature is reached.

A TPI room thermostat will have 100% demand when the system first calls for heat. When the room temperature approaches the set point, it then calculates how many minutes are required within each firing period to satisfy the set temperature. The TPI thermostat will then reduce the firing time in that cycle period in proportion with the demand. This means that as the room temperature approaches set point, the boiler is fired progressively less.

See also: http://www.transcat.com/PDF/PIDControl.pdf

I don't see why you should make those assumptions. There is a minimum firing time (normally one minute). So if there is a 10 minute cycle and the ON period is less than 10% the boiler should still fire for one minute.

I suspect that if the ON period is between, say 5%, and 10% the boiler will fire for one minute and below 5% it will not fire at all. This is based on the fact that my system can go for over 10 minutes without the boiler firing at all.

I agree, this is quite possibly what it does. So, when the heating demand is low (mild outside), the controller may be dropping out of the proportional band and then back in when the temperature drops. This could explain operation seen by the OP where the heating stays off for a long period and the temperature drops perceptibly, because the controller is not operating in the PI control band.

 

[D_Hailsham]

No, there isn’t a constant output, but the time averaged output of the system when working in time proportional mode can be constant.

Agreed.

See also: http://www.transcat.com/PDF/PIDControl.pdf[/QUOTE]
A good explanation - they are very difficult to find.

I agree, this is quite possibly what it does. So, when the heating demand is low (mild outside), the controller may be dropping out of the proportional band and then back in when the temperature drops.

Why would it drop out of the proportional band just because it is mild.

The smallest proportional band is 1.5°C, so even if it is 18°C outside, you will still be operating within the proportional band with a Target temperature of 20°C.

 

[mikely]

Why would it drop out of the proportional band just because it is mild.

In mild weather, when the heat demand required to maintain the internal temperature is low, the system will be operating at the top of the proportional band, close to zero output. If the unit always uses a 1 minute minimum on-time and 6 cycles per hour, the minimum output it can use is 10%. If the PI controller has determined that it only needs an output of 5%, what does it do? It could increase the cycle time to 20 minutes or more, or it could just turn off and wait for the temperature to drop.

In effect the proportional band would not be a straight line gradient between 100% and 0; it would drop to zero once it reaches 10%. This is what I meant by ‘dropping out’ because the output demand has dropped to zero.

 

[D_Hailsham]

In mild weather, when the heat demand required to maintain the internal temperature is low, the system will be operating at the top of the proportional band, close to zero output. If the unit always uses a 1 minute minimum on-time and 6 cycles per hour, the minimum output it can use is 10%. If the PI controller has determined that it only needs an output of 5%, what does it do? It could increase the cycle time to 20 minutes or more, or it could just turn off and wait for the temperature to drop.

In effect the proportional band would not be a straight line gradient between 100% and 0; it would drop to zero once it reaches 10%. This is what I meant by ‘dropping out’ because the output demand has dropped to zero.

But this can be true even when it is very cold!

The proportional band is just the temperature range, below the set temperature, over which the boiler output is varied. If the difference between Actual and Target is greater than the PB, the boiler will run 100%. If the Actual is 50% of the PB below Target, it will fire 50% of the time. It doesn't matter if it's mild.

There is a question over what happens if the required firing time is below the one minute minimum. Does it run for one minute every cycle or does it miss a turn? I suspect it misses a turn - or drop out, as you call it.

When I've nothing better to do, I'll sit by the boiler and monitor it!

 

[mikely]

I think you are not accounting for the integral action of the controller. The proportional band will not normally be entirely below the set temperature, but around it.

Untitled

• mikely
• 2 Nov 2011
• 1

Referring to the diagram, in this example the controller is initially set up so that the target temperature Ts is at the top of the proportional band PB. When the temperature reaches (Ts – PB), the system output starts to reduce and will stabilise at some temperature T1 where the output (30% in this example) is sufficient to balance the heat loss. The system will not reach the target temperature because its output is constrained by the position of the proportional band. There will be an error e = (Ts - T1). However, the integral action of the controller eliminates this error by pushing the proportional band up to the position PB’ where the target temperature is achieved (at a slightly higher output of 35%, because it takes more heat to maintain a higher temperature).

The position of the proportional band with respect to the target temperature will depend on the heat demand required to maintain the target temperature, which is effectively a measure of how cold it is outside. When it is mild, the target temperature will be close to the top of the proportional band because the output demand will be low. This is where we get into the issue of how does the controller output respond when it only requires a very low output.

 

[D_Hailsham]

I think you are not accounting for the integral action of the controller.

...

There will be an error e = (Ts - T1). However, the integral action of the controller eliminates this error by pushing the proportional band up to the position PB’ where the target temperature is achieved (at a slightly higher output of 35%, because it takes more heat to maintain a higher temperature).

I can understand that, but I'm not sure that it's correct to say that the Integration part of the process moves the band up/down, parallel to the original band. Couldn't it also change the slope of the band?

 

[mikely]

I can understand that, but I'm not sure that it's correct to say that the Integration part of the process moves the band up/down, parallel to the original band. Couldn't it also change the slope of the band?

The slope of the proportional band is effectively the gain of the proportional term of the controller. So with a proportional band of 1.5°C, the gain is 66% change in output per °C of error. When changing the proportional band parameter, you are changing the proportional gain of the control system and thereby changing the dynamic response of the system. The integral term of the controller removes the static error over time and ensures the long term control accuracy. Have a look at the description of Reset (Integral) Control Action in the Transcat note.

I should add that I can claim no knowledge of quite how Honeywell implement their controllers, so my descriptions are based on my understanding of the principles of PID controllers in general.

 

[D_Hailsham]

The slope of the proportional band is effectively the gain of the proportional term of the controller. So with a proportional band of 1.5°C, the gain is 66% change in output per °C of error. When changing the proportional band parameter, you are changing the proportional gain of the control system and thereby changing the dynamic response of the system.

Agreed, but the initial setting is only an approximation of what the correct gain should be.

The integral term of the controller removes the static error over time and ensures the long term control accuracy.

Agreed, but there is more than one way of doing this; e.g the red line.

Untitled

• D_Hailsham
• 3 Nov 2011
• 1

 

[mikely]

It would be possible to do what you suggest, but you are then using the integral action to change the proportional gain of the system which will then affect the dynamic response. This would not normally be desirable.

 

[D_Hailsham]

It would be possible to do what you suggest, but you are then using the integral action to change the proportional gain of the system which will then affect the dynamic response. This would not normally be desirable.

But you can't assume that the initial proportional gain is correct; P and I are interdependent.

The correct values will depend on the characteristics of the building whose temperature you are trying to control (insulation and thermal capacity) and the tolerance within which you wish to control the temperature.

 

[mikely]

But you can't assume that the initial proportional gain is correct;

No, although the proportional band is a selectable parameter on the Honeywell controllers, so I would think that it is a fixed value. If it was a value that the controller determined for itself, there would be no point in it being user selectable.

The Honeywell specification for the CM907 describes that the proportional band:
Can be adjusted up to 3C (default is 1.5C) to provide better temperature control (less overshoot).
Useful for:
a. Well insulated homes with over-sized heating systems.
b. Air systems with fast response

Which is what you would expect. If the system has a more rapid response, you want to reduce the gain (increase the proportional band) to reduce overshoot.

P and I are interdependent.

They will interact, but only through their effect on the controller output and the resulting feedback.

The correct values will depend on the characteristics of the building whose temperature you are trying to control (insulation and thermal capacity) and the tolerance within which you wish to control the temperature.

Indeed, and I would expect that this is where the ‘learning functions’ of the controllers will have an effect. For instance when the thermostat starts a new heating period, it would use settings that it has learnt from the previous heating period(s).