Hi,
I have a Cert of Lawfulness on a hip to Gable Loft conversion, on a semi detached house.
My architects calculations on the plans show an increase of 48.28 cu mt.
The councils 'delegated report' calculates an increase of 40.9 cu mt.
I went to the council - but they refused to run through how they calculated that figure.
I have checked the dimensions of the plans at 1:50, and they look correct.
I cannot work out what my architect has done with the hip to gable volume calc:
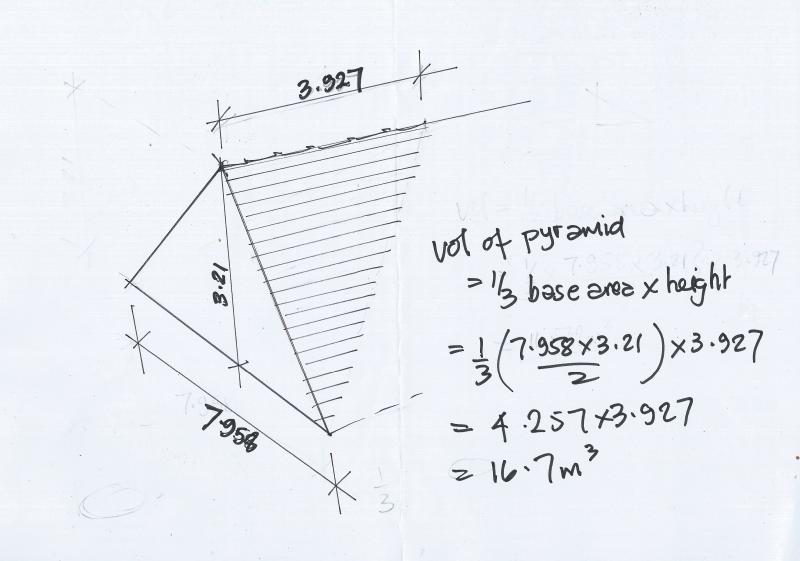
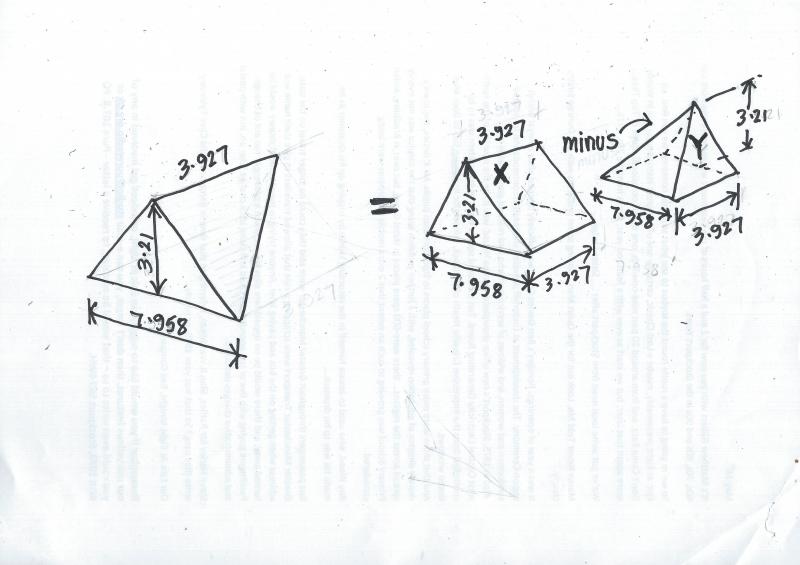
7.958 long x 3.210 high = 25.54m2 divide by 2 = 12.77 m2 x 3.927 ridge length = 5.16 m3 divided by 2 = 25.08m3
Its not how I would do it, I'd use:
Finished Gable volume: bhl/2
(ie (7.958x3.210x6.257) divide by 2 = 79.91
Existing Hip Volume: bhl/4
(ie (7.958x3.210x3.297) divide by 4 = 21.05
Plus remaining gable:
Existing Ridged Part Roof Volume:
(7.958x3.210x3.297) divide by 2 = 50.15
So 21.05+50.15=71.20
79.91 less 71.20 = 7.99 cu mt
So I make the hip to gable enlargement 7.99 cu mt, my architect 25.08 ... who is right.
Thanks
I have a Cert of Lawfulness on a hip to Gable Loft conversion, on a semi detached house.
My architects calculations on the plans show an increase of 48.28 cu mt.
The councils 'delegated report' calculates an increase of 40.9 cu mt.
I went to the council - but they refused to run through how they calculated that figure.
I have checked the dimensions of the plans at 1:50, and they look correct.
I cannot work out what my architect has done with the hip to gable volume calc:
7.958 long x 3.210 high = 25.54m2 divide by 2 = 12.77 m2 x 3.927 ridge length = 5.16 m3 divided by 2 = 25.08m3
Its not how I would do it, I'd use:
Finished Gable volume: bhl/2
(ie (7.958x3.210x6.257) divide by 2 = 79.91
Existing Hip Volume: bhl/4
(ie (7.958x3.210x3.297) divide by 4 = 21.05
Plus remaining gable:
Existing Ridged Part Roof Volume:
(7.958x3.210x3.297) divide by 2 = 50.15
So 21.05+50.15=71.20
79.91 less 71.20 = 7.99 cu mt
So I make the hip to gable enlargement 7.99 cu mt, my architect 25.08 ... who is right.
Thanks