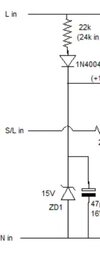
Someone has asked me, off list, to explain the reason for the above - so, in case anyone else doesn't know, but would like to ...
.... I hope that may possibly afford a little help to at least some people!
I have been asked, again 'off-list' for further explanation/clarification.
To 'properly' address the maths, and literally consider the instantaneous voltage of an AC waveform
"at every point in time" requires some understanding of calculus, which not everyone will have. However, what I can do is illustrate what happens if one consdiers 'many points in time', and then further illustrate what happens as one increases the number of those 'many points in time', and therfeore approaches what calculus would do.
The first table below considers a sine-wave waveform with a peak voltage (both positive and negative) of 339.41 V. It shows the instantaneous voltage at 1 mS intervals during one complete cycle. It also shows that instantaneous voltage 'squared', and hence calculates the mean (average) of those squared voltages over the whole cycle and, finally, the square root of that mean is taken to result in the RMS figure. It then shows exactly the same for a half-wave-rectified version of the same sine wave.
As can be seen below, that results in figures for the RMS of 234.22 V for the full waveform and 165.62 V for the half-wave one - figures which are a little lower than the theoretical ones (240.0V and 169.7V respectively).
It would obviously be tedious to post similar (very lengthy) tables in which the instantaneous voltage was considered more frequently than once every millisecond, but the second table (below) shows the answers. As one reduces the interval between one's 'look at the voltage' the calculated RMS gets gradually closer to the theoretical figures, which it actually hits (to 3 decimal places) when one looks at intervals of 0.1 ms or less. This is the same as what calculus would do, effectively considering an infinite number of infinitely small time intervals.
Again, I hope that might be of some help to some people.
Kind Regards, John